A hypercube full of rooms
While I'm on the subject of Dungeons & Dragons (see my previous post on ability score probabilities), I recall something I did involving a tesseract way back in 2007 and posted on the community forum of Wizards of the Coast. WOTC took down their forum in 2015, but fortunately the Wayback Machine has an archived copy.
Imagine a cubical room. It has four walls, a ceiling, and a floor (six faces). Each face has a door or opening, to allow you to pass through to the next room. Each cubical room connects to six other rooms — but there are eight rooms interconnected this way.
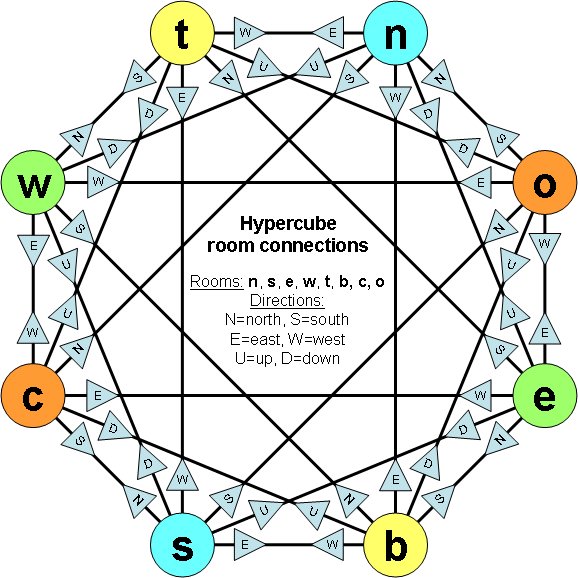
This isn't possible to draw in 3 dimensions without distorting some of the rooms. Imagine a central room with a room connected to each face. So you have the center room, the north, south, east, and west rooms, and the top and bottom rooms. That takes care of seven rooms. The eighth room, we'll call it the "outer" room, is connected to those six rooms surrounding the center. Designating the rooms as c, n, s, e, w, t, b, and o, respectively, the connections aren't really apparent:
t
n /
\ / o
w -- c -- e
/ \
/ s
b
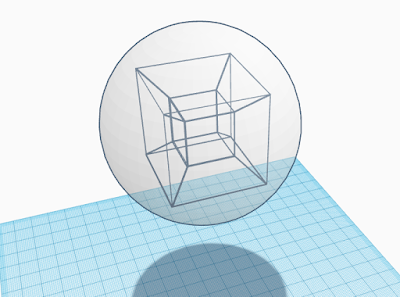
A way to visualize this is to imagine a cubical center room surrounded by six distorted rooms. The outer faces of the six distorted rooms form the faces of the outer room, which can be imagined as an inside-out cube. In this picture, this outer room is displayed as a sphere, which isn't really a boundary, just a designation of some volume of space. The only surfaces of this volume are actually the square surfaces facing inward to the six rooms shaped like truncated pyramids.
By the way, I created that image using Tinkercad, a 3-D design and modeling tool that works in any browser.

A tesseract illustrating the concept of pushing a middle layer room toward the center.
Source: JasonHise on Wikimedia Commons
We can see from the figures above each room touches six others. Put another way, each room doesn't touch one other:
- c doesn't touch o
- t doesn't touch b
- n doesn't touch s
- e doesn't touch w
Each cube also has the same connection diagram as the center cube. You can swap any two non-touching cubes, such as c and o, leaving the rest of the diagram alone. Or you can push one of the middle-layer cubes into c's position, which would push the opposite cube into o's former position, and o would move into the middle-layer position vacated by the original cube that you pushed to the center position.
Knowing these things, here's perhaps an easier way to visualize a hypercube of rooms. We can simply draw a connection diagram of all the rooms in a hypercube. I've drawn this as an octagon with the isolated pairs of rooms at opposite corners.
Each room connects to six others in the directions, north, south, east, west, up, and down. Some observations:
- If you start in any room, pick a direction, and keep going in that direction, you will have visited four rooms, traversing a rectangle in the diagram (or a square if you choose up or down).
- I imagine that if you pick a direction and just stand in the doorway looking in that direction, you will see an endless tunnel of doorways extending to infinity, and you would see yourself standing in every fourth doorway.
- If the trap doors in the floor and ceiling are open, then a ball dropped into the floor opening would pass through three other rooms and return to the original room, falling again through the opening in the floor, forever or until air currents cause its trajectory to intersect the edge of the opening.
In the context of Dungeons & Dragons, the Dungeon Master running the game can create an interesting experience for the players if each of the 8 cubes acted like a normal room, with gravity in one direction, definite compass directions, and ladders or stairways connecting floor and ceiling openings.
If the party decides to go through the west door of each room, after passing through four doors they'd find themselves in the same room they started in. Even more dramatic, if a player falls through the hole in the floor, after a little while the same player will fall through the ceiling of the same room, and keep falling forever unless someone catches the poor fellow. The video game Portal let a player make use of this construct: Given portal in the floor and in the ceiling directly overhead, if you fall into the portal in the floor, you fall out of the one in the ceiling, back through the one in the floor, endlessly.
I can imagine such a hypercube being the home of a powerful hermit wizard, who enters and exits by way of a portal. Each room could have a specific function: bedroom, privy, bath, kitchen, laboratory, dining room, storage room, living/dining room, all appropriately trapped and alarmed against intruders, with a well-hidden exit portal, and a harrowing encounter with the owner intent on defending his home.
Comments
Post a Comment