My favorite mathematical card trick
![[deck of cards]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEib2OoH-Mu6zbD0jM_CCqRvYNnjlYb-9l83gdFcQdsV1OE1e8ZN9YsXW55PJscBBJ68eotb59jVEnbx9CDcgVPP9fPKtNCZ362OXRvmCUS7XIsbLRkEC_Xg9lkQaLJHTPB4jW3NoVLTW3g/s320/cards.jpg)
I learned this card trick in the fourth grade, decades ago, before the World Wide Web existed. I have never seen it written about, and anyone to whom I have shown it has never seen it either. This is surprising given how long I've known this trick. Did a brilliant classmate (or a parent) invent it? I'd love to know the origin.
This is a mathematical card trick. Meaning, there is no sleight of hand, no actual trickery, just manipulation of playing cards that gives a surprising, final result. You can find many examples of mathematical card tricks on the internet; some of them appear downright magical and quite impressive.
What the audience sees
Here is how this trick appears to the audience. It looks like many steps, but they are easy to remember after you've practiced the trick even once:
- Starting with a deck of 52 cards (no jokers), you ask a volunteer from your audience shuffle the deck.
- You deal out the cards into seemingly arbitrary face-up piles, handing the last few cards to the volunteer to hold.
- You turn the piles face down, and tell the volunteer to pick up any piles randomly until three piles are left.
- You arrange the remaining three piles in a row, offer to rearrange the positions of the piles, and turn the top card of the pile on each end face up. The top card on the middle pile remains face down.
- Tell the volunteer that you can predict the value of the middle face-down card with the volunteer's help.
- Have the volunteer discard ten cards from those in hand.
- Tell the volunteer to add the values of the two face-up cards, and discard that many from those still in hand.
- Predict that the remaining cards in the volunteer's hand is the value of the remaining face-down card on the middle pile.
- The volunteer counts the remaining cards and reveals the card on top of the middle pile. Your prediction was correct!
With the right patter, this trick can be orchestrated to amaze the audience.
Secret sauce
What makes this trick work is the way in which you deal out cards into piles. You can explain to the audience what you're doing because it isn't apparent how the method could possibly guarantee the final outcome of the trick, but you may decide it's best to leave them in the dark. Here is how I learned it:
- Deal a card face up to start a pile. If it's a face card, put it back in the deck and deal another.
- The value of this first card is the start of a count up to 13. Continue dealing out cards face up until reaching a count of 13. For example, if the first card of the pile is a 9, then count 10, 11, 12, 13 as you deal four more cards onto the pile. The values of these additional cards don't matter. Only the first card value matters, for determining the size of the pile.
- Upon reaching a count of 13, start a new pile the same way.
- Keep making new piles until you run out of cards. If you don't reach 13 on the last pile, have the volunteer hold onto those extra cards.
Misdirections
I had been performing that trick as a child and into my adulthood never really knowing how it works. There are two unnecessary steps, likely put there for the purpose of misdirection.
First, did you notice that ten cards got discarded in step 6? If you start out with a deck of 42 cards, that step is unnecessary. In fact, I eliminated this step years ago whenever I have performed this trick. I first prepare the deck by discarding 10 face cards, leaving 42 cards in the deck.
Another element of misdirection is dealing out the whole deck into several piles of cards, instead of stopping at three piles. Going through the whole deck isn't necessary for the trick to work mathematically, but it is necessary for enhancing the mystery to the audience. That is, creating more piles than required provides a useful illusion of giving more choices to the volunteer, to decide which three piles to use in the trick. It doesn't matter which three piles are chosen.
If you're a slow dealer, you risk boring the audience watching you deal cards one at a time from a whole deck. So you may want to stop at three piles, but have the volunteer shuffle the deck before making a new pile, to add to the illusion of randomness. If you can deal out cards reasonably quickly, going through the whole deck is fine. I personally think it's better to give the volunteer plenty of piles to choose from.
Analysis
I wondered, why does it work with 42 cards, and can it be made to work with the full deck somehow?
Let's ignore the ten discarded cards and assume we start with a deck of 42 cards.
Call the three remaining piles 1, 2, and 3. Let's say \(f_1\), \(f_2\), and \(f_3\) are the values of the first card in each of the piles.
Because we count from the value of the first card up to 13, the number of cards in each pile is:
$$\begin{array}{rl} n_1 & = 13+1 - f_1 \quad = 14 - f_1 \\ n_2 & = 14 - f_2 \\ n_3 & = 14 - f_3 \end{array}$$For example, if the first card in a pile is 🂸 (8), then there are six cards (14−8) in that pile, as a result of the counting 8, 9, 10, 11, 12, 13.
Because we started with 42 cards, the number of cards \(n_h\) in the volunteer's hand is:
$$\begin{array}{rl} n_h & = 42 - (n_1 + n_2 + n_3) \\ & = 42 - \left[(14 - f_1) + (14 - f_2) + (14 - f_3)\right] \\ & = 42 - (42 - f_1 - f_2 - f_3) \\ & = f_1 + f_2 + f_3 \end{array}$$In other words, in step 3, the volunteer ends up holding the same number of cards as the sum of the first card of each pile on the table! And because you turned the piles face down in step 3, these first cards are now on top of each pile.
Therefore, in step 7, when the volunteer discards a number of cards equal to the sum of two cards on the pile, the number of remaining cards is always the the value of the remaining face-down card on top of the middle pile, because the volunteer was holding the total of all three values.
Generalization
We can generalize this trick to use other values for the initial size of the deck, as well as the number of piles.
Let's rewrite the equation for the number of cards in each pile:
$$n_1 = m + 1 - f_1$$ $$n_2 = m + 1 - f_2$$ $$n_3 = m + 1 - f_3$$where \(m\) is the maximum counting value. In the version of this trick described above, \(m = 13\), and the size of each pile is 13+1 minus the value of the pile's first card.
The starting size of the deck is just \(n_d = 3(m+1)\), which is 42 for \(m = 13\).
If the maximum count value of each pile is 16 instead of 13, then \(m=16\) and the size of the deck must be 3×(16+1) = 51 cards, requiring you to discard only one card from a standard 52-card deck before starting the performance. Going the other direction, a maximum count value of 10 requires a starting deck of 33 cards.
We can also design this trick for an arbitrary (within reason) number of piles left on the table. The general formula for number of cards required in the deck becomes:
$$n_d = p (m+1)$$where \(p\) is the number of piles left on the table.
So there is a way to perform this trick using a complete 52-card deck: Your maximum counting value is 12 and you leave four piles on the table; that is, \(m=12\) and \(p=4\). In this case, you would tell the volunteer to turn up the top card on any three of the four piles (more generally, turn the top cards face up on \(p-1\) piles), calculate the sum, and discard that many cards, revealing that the number of cards remaining equals the value of the top card on the fourth pile.
In the trivial case of one pile, provided you set \(m\) so that you can actually get one pile, you don't turn any cards face up (because \(p-1\) piles is zero piles). The card that starts the pile is always equal to the number of cards left in the volunteer's hand. For example, with \(p=1\) and \(m=10\), the initial size of the deck must be 11 cards. If the first card of the pile is an ace 🂡 (value 1), then the pile would have 10 cards, leaving one in the volunteer's hand — equal to the value of the first card. If the first card is a five 🃅, then the pile has six cards in it, and five are left in the volunteer's hand.
Final thoughts
You can also start a pile with a face card if you decide in advance what values to assign them. If the game of Blackjack is familiar to your audience, you can assign all face cards a value of 10. Or, you can give them any values (for example 11, 12, 13 for jack, queen, king) as long as you use those values consistently throughout the trick.
When performing this trick for young children, however, it's best to eliminate the face-card abstraction and just start each pile with a numbered card.
I cannot imagine how anybody thought up the original trick as I was taught by a fourth-grade classmate.
Oooh <3
ReplyDeleteI went on a quest printing the perfect shopping bag handle for my sister with severe arthritis and stumbled upon your ergonomic handle OpenSCAD script @thingi..
A really well documented project to accompany the script, 11/10 cups of coffee in my hall of fame.
Entering your blog I instantly saw this post and thought for myself, that it can't be..!?
But yes, indeed, the very same 'magic' ;0)
I learnt this as a kid in the 79/80-ish here in Sweden, and still do this amazing trick on amazed kids..
You are the first one I know (besides my mentor) who knew about this.
So it's international, and not just a really local phenomena.
Take care,
../Patrik
Hi Patrik. I know I'm dating myself when I say this, but I remember learning this trick in 1969. A classmate taught it to me. It wasn't until decades later that it occurred to me to generalize it so it would work with a full 52-card deck.
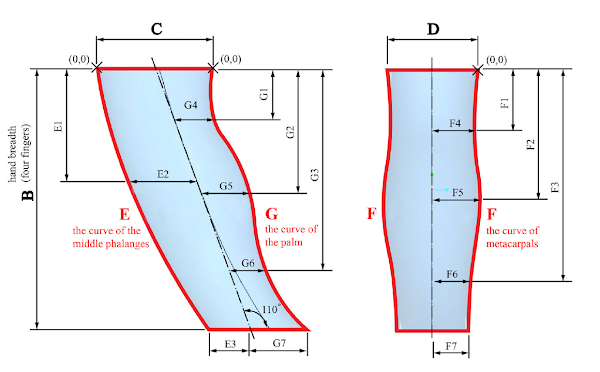
DeleteAs for the handle at https://www.nablu.com/2022/03/whose-hands-are-biggest-you-may-be.html - if you're going to have only pulling loads, all you really need is a symmetrical bar that bulges in the middle, like an ellipsoid. It should probably have an elliptical cross section like my handle. You could use my handle too, with a tilt angle of 90° instead of 110°, but then you'd have to pay attention to which end of the handle is for the top of the hand versus the bottom of the hand. A shopping bag handle should probably be symmetrical so you can grab it from any direction.
Thanks Alex for the suggestion.
DeleteBecause of the arthitis lil' sis have accumulated, I'll opt fot the best fit on behalf of more practical.
Since my OpenSCAD-Fu is really limited beyond the basics I think I'll export and edit the mesh.
Make it curved in the ends and add a happy arrow as a clue for her :0)
Once again, your write-ups really really rock.
Well balanced tech/humor for a rook in respective field (read them all now, amusing).
../Patrik
Patrik - please write to me at anachronist -at- gmail.com. I can send you a correct STL. Also I am thinking of designing an ergonomic handle specifically for bags.
Delete